[2D Geomtry] 二維線段交點

在本篇 entry 我們談一談二維線段交點求解方法
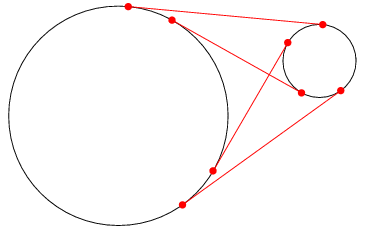
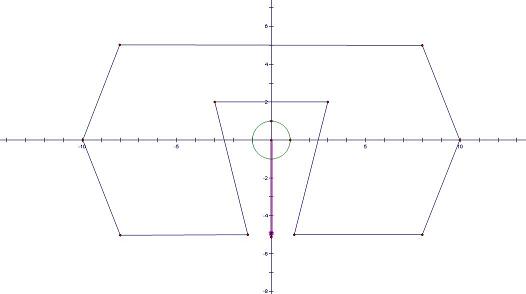
本人認為，最後討論的 "三角形面積方法" 的解相當優美

---

直線方程組方法

中學時期，我們都學過用聯立方程組求 線 / 線交點：

A x + B y = C
D x + E y = F

可這個方法缺點是
用代入法 (substitution) 或消元法  (elimination) 求出的一般解
在 x系數 = 0 或 y系數 = 0 的情況需要特別分開處理

我們亦不能單從 solution
簡單判斷交點 Q 是否在線段 AB 或 CD 之內

---

向量方法

這是在 year 1 暑假 ACM training 時學會的
感覺相當強大、漂亮

將兩條線段表示成：

P₁ = A + s AB -------- (1)
P₂ = C + t CD -------- (2)

其中 s, t 分別是 線段AB,CD 的參數

[Hard 2D Geometry] Ural 1464 Light

• 題目在此 

---

這是前幾天在 Timus OJ 的題目分類，按下 Geometry
隨機選擇的一題... (我喜歡隨機選題...)

讀完題目，感覺是經典題目... 但沒有想法...
細心一看... 原來這題還有另一個 Tag ── Hardest Problem
再一看 Accept Rate... 3%

後來跟 Joe 討論過一下，他一兩天就 AC 了...
但他說未能用 STL 的 set implement，只能徒手寫 Heap

(在 Joe 詳細地講解完算法以後)
於是便試試用 STL implement... 結果成功了 !!
不過代價是筋疲力竭
算法雖然直觀，但在處理 ordering 的過程 (見下) 是無限的 confusion + frustration...
而且，最後還要調 epsilon 才通過... (角度 radian, 1e-10)

---

Problem Statement：

給一個簡單 (Simple) N邊形 (N <= 500000)
在其內部放一個點光源 (Strictly inside)
問，光源照到的面積為何？

[2D Geometry] 內/外 兩圓公切線 的對應

2010-08-23 2am 更新：

1. 兩種 圓/圓公切線 (Common Tangent)，正名為
   a) 「外公切線」(Common External Tangent)， 及
   b) 「內公切線」(Common Internal Tangent)
   下面討論一律略去「公」 ("Common") 一字
   ....嗯... 外公切線... 以下簡稱為「外切線」及「內切線」
2. 兩圓切線共有 5種情況 ...
   我正在驗證本 Entry 所提供的 Implementation 能否覆蓋全部情況
   ──別被嚇到... 本人直觀地認為本 Entry 所討論的 Implementation
   已能覆蓋所有情況，只是仍有待證實

---

昨晚隨便在 Ural Timus OJ 上選了一道幾何 ── Ural 1340 Cucaracha
想出了某 case 的算法後
發現自己不懂怎樣計算某一角度
只懂得 BSearch... 然後又發現 BSearch 不行...

再細心一想
才發現這個問題其實可以 reduce 至「點到圓切線」...

---

那我就想起... 原來我還沒有一份「點到圓切線」的 Code Template...

在這次之前不知道推導過這公式多少次...
雖然每次都能推出，但推導過程會花費相當長的時間
所以實在太有必要寫一份武器（要不，就把公式推導到爐火純青的熟練程度）

上回在 這篇Entry 談過
「點到圓切線」是「圓到圓切線」的特例 ── 其中一圓半徑=0

而「圓到圓切線」在一般情況下共有 4條

 

分 「外切線」(External Tangent) 及 「內切線」(Internal Tangent) 兩種

──註：上行此兩項述語這是本文的定義，自行定義的原因一是為方便以下的說明
二是因為在 Google 暫時搜不出相關的述語...

而每種切線各有 2條

那 code template... 就是寫！

寫呀寫的...
突然有一個驚喜的新發現（潮左勿 WoW）：

「內切線」原來是「外切線」的特例！

Voronoi diagram, Delaunay triangulation and 3D Convex Hull

(Still refinining... this blog entry. More images will be added to aid understanding... hopefully)

Introduction:

In the following discussion, Voronoi diagram and halfplane intersection refer to the 2D case, unless otherwise specified.

I hope I can list some nice properties of as well as some relationships between the following three structures in computational geometry:

• Voronoi diagram
  
  
  
  [You need to understand what is going on on the right image.The left and the middle will be discussed below.]
• Delaunay triangulation
• 3D convex hull 

[隨筆] 修煉 I - Rotating Caliper

這幾天正在忙 research
亦有一邊做題目

不過要下決心不做水題了... orz

這陣子...

Chin 經已把 Farey Sequence 弄明白
CTLi 則在攻 Game 及 插頭DP 的題目
Joe 也剛剛應用 Sweep Line Algorithm 把 Chengdu 2008 的 題D 幹掉

我呢...?
也許是時候開始研究 旋轉卡殼(Rotating Caliper) 及 凸多邊形(Convex Polygon) 了

感覺這個 topic 的資訊量挺大的 (見下) ...

[舊帖] UVa 11275 3D Triangles

Old Post in Xanga on 2010-02-18

---

Problem Statement:
Given 2 triangles in R³, check whether they share at least 1 common point.

---

今日 Research 有 3D 野要搞...
Google... 無意間見到 一個 theorem - SAT (?)
原 來 SAT = Separating Axis Theorem

發覺 ACM 可能有用喎!

應 用落呢題之後... Runtime 快過以前 Ray / Plane Intersection !
而且對比之下, 呢個方法更加 mechanical, 貌似好多地方都用得著

PKU 2036 I Conduit!

題意：

在白紙上要畫 N (≤ 10000) 條線段 (Straight line segment)，問總共最少要畫多少筆

---

解1：

排序→掃描 (Vector Arithmetic)

出現在同一筆的線段，必然有同樣的斜率（或角度）
對於相同斜率但不共線的線段
它們與原點（或任意 Fixed 的一點）有不同的距離

PKU 2416 Return of the Jedi

題意：

在平面上，給定 N (≤ 10) 個圓（任何兩圓不相交／觸碰）
及 A、B 兩點

求最短 A 到 B 路徑（不得進入任何圓形內，但可以觸碰）的長度

---

應用知識：

此題基本上是一道 2D Geometry Exercise
只是在 公式推導 及 處理 Boundary Cases 時要比較小心...

1. 圓到圓切線（全４種）
2. 點到圓切線
   
3. 判斷 線段／圓 交點
   
4. 最短路算法

2. 的計算可透過 1. 完成
── 把 點 看為 半徑 = 0 的圓

---

PKU 3703 Intuition of Escape

題意：
二維場景內
給定一個 半徑 = R，位置 = (0,0) 的圓
及 N 個多邊形障礙物
問，是否在存一個移動方向，使得當圓形以直線前進時
不會觸碰這些障礙物

分析：
算法大約都是枚舉（離散的）移動方向/角度 - angle[M]
然後逐一判斷是否可行

有關「觸碰」的限制
雖然可以 ± Epsilon 處理
但這會令代碼變得噁心

ICPC 4612 Fractal

[舊題重做]

題意：
給定 N 點定義 (上例 N = 4) 一條 polygonal line sequence
以此圖形作基礎作 D 層的分形
由起點至開始遍歷 d ( 0 <= d <= 1) 的部份 (d = 0: 起點; d = 1: 終點)

求終點座標

算法：
直接分治：
Point2D f(double d, int depth)

f ( d, depth ) --> f( d, depth + 1) ...