[2D Geometry] 內/外 兩圓公切線 的對應

2010-08-23 2am 更新：

1. 兩種 圓/圓公切線 (Common Tangent)，正名為
   a) 「外公切線」(Common External Tangent)， 及
   b) 「內公切線」(Common Internal Tangent)
   下面討論一律略去「公」 ("Common") 一字
   ....嗯... 外公切線... 以下簡稱為「外切線」及「內切線」
2. 兩圓切線共有 5種情況 ...
   我正在驗證本 Entry 所提供的 Implementation 能否覆蓋全部情況
   ──別被嚇到... 本人直觀地認為本 Entry 所討論的 Implementation
   已能覆蓋所有情況，只是仍有待證實

---

昨晚隨便在 Ural Timus OJ 上選了一道幾何 ── Ural 1340 Cucaracha
想出了某 case 的算法後
發現自己不懂怎樣計算某一角度
只懂得 BSearch... 然後又發現 BSearch 不行...

再細心一想
才發現這個問題其實可以 reduce 至「點到圓切線」...

---

那我就想起... 原來我還沒有一份「點到圓切線」的 Code Template...

在這次之前不知道推導過這公式多少次...
雖然每次都能推出，但推導過程會花費相當長的時間
所以實在太有必要寫一份武器（要不，就把公式推導到爐火純青的熟練程度）

上回在 這篇Entry 談過
「點到圓切線」是「圓到圓切線」的特例 ── 其中一圓半徑=0

而「圓到圓切線」在一般情況下共有 4條

 

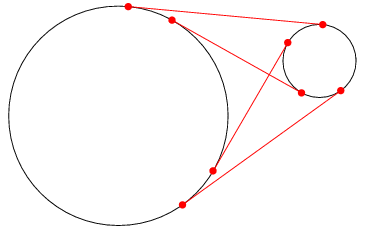
分 「外切線」(External Tangent) 及 「內切線」(Internal Tangent) 兩種

──註：上行此兩項述語這是本文的定義，自行定義的原因一是為方便以下的說明
二是因為在 Google 暫時搜不出相關的述語...

而每種切線各有 2條

那 code template... 就是寫！

寫呀寫的...
突然有一個驚喜的新發現（潮左勿 WoW）：

「內切線」原來是「外切線」的特例！

---

「內切線」與「外切線」計算的對應：

設輸入為：

• 圓1 := (圓心 p1, 半徑 r1)
• 圓2 := (圓心 p2, 半徑 r2)

「交切線」算法 ── ComputeCircleInternalTangent(p1, p2, r1, r2)
可以 reduce 至
「外切線」算法 ── ComputeCircleExternalTangent(p1, p2, r1, r2) ：

Function ComputeCirleInternalTangent(p1, p2, r1, r2)     Return ComputeCircleExternalTangent(p1, p2, -r1, r2) EndFunction

為甚麼？

怎麼發現？

這樣可以大幅減省 code length !!

然而，上述算法還有一個問題要 settle：
對於「外切線」 及 「內切線」算法
其實各自有 undefined 的 condition：

• 當 圓1 完全包含 圓2 (或相反)，「外切線」不存在
• 當 圓1 與 圓2 相交時，「交切線」不存在

所以在 Function call 的 implementaion 中
需額外加一個 If 判斷...

但是，很快我又立刻發現
這種條件對於「內切線」及「外切線」 而言也是一一對應的
而且，是跟 reduction 那般一一對應！

（您：... ... 啥？甚麼跟甚麼呀？）

呃... 好... 容許我再更仔細的說明：

---

「內切線」與「外切線」Undefined condition 的對應：

(註1： 如果以下的看不懂，不打緊
(用紙筆多畫幾個 example，把 兩個圓心用直線連起，就會明白)

重溫 Undefined condition：

1. 「外切線」不存在
   ⇔ 圓1在圓2之中（或相反，圓2在圓1之中）
   ⇔ 圓心距離 < 半徑之差
   ⇔ || p1-p2 || < || r1-r2 ||
2. 「內切線」不存在
   ⇔ 兩圓正規相交（i.e., 重疊Area > 0）
   ⇔ 圓心距離 < 半徑之和
   ⇔ || p1-p2 || < r1+r2

(註2： 以下的解釋有點長... 但大意只需用眼 Diff 一下就會知道...)

Implementation 大約是：

Function ComputeCircleExternalTangent(p1, p2, r1, r2)     If  || p1-p2 || < || r1-r2 ||         Return Undefined     EndIf     /* Vector arithmetic here... */ EndFunction

Function ComputeCirleInternalTangent (p1, p2, r1, r2) /* From last section */     If  || p1-p2 || < r1+r2         Return Undefined     EndIf     Return ComputeCircleExternalTangent(p1, p2, -r1, r2)  // ------- (*) EndFunction

發現了沒？

(*) 那裏 呼叫 ComputeCircleExternalTangent 所 execute 的 If statement
    || p1-p2 || < || -r1-r2 ||
跟 (*) ComputeCirleInternalTangent 裏的 If 等價的：
    || p1-p2 || < r1+r2

所以，在 ComputeCirleInternalTangent 的 If 可以刪去！

最後得出簡化的 Implementaion：

Function ComputeCircleExternalTangent(p1, p2, r1, r2)     If  || p1-p2 || < || r1-r2 ||         Return Undefined     EndIf     /* Vector arithmetic here... */ EndFunction

Function ComputeCirleInternalTangent(p1, p2, r1, r2)     If  || p1-p2 || < r1+r2         Return Undefined     EndIf     Return ComputeCircleExternalTangent(p1, p2, -r1, r2) EndFunction

---

原理：

上述的「對應」一定有其數學原因...
我還沒有完全證明出來
但我相信，以下直觀的說明與背後原理八九不離十：

(待追加)

---

結語：

「內切線」的計算可由「外切線」的計算完成，所以：

• 對於計算兩圓 全部 4條公切線 (或偵測其不存在)，一道公式便足夠矣

那...「內切線」與「外切線」這對應
是怎樣發現的？
我把兩個 function 寫了出來，眼看發現相似
最後用 program diff 一下...
──詳細公式推導... 有機會可以再寫...

...!!

然後... 就寫了這篇 Entry

---

Offtopic：

1. 多個橢圓相關定理
2. 以後可以考慮 用PPT繪圖

---

按：

似乎寫得太長... 太多 term...
寫到很複雜的樣子
實在擔心 有心閱讀本篇 entry 的讀者 (假若存在) 會「見木不見林」

大家可以給些意見嗎 @@