PKU 3703 Intuition of Escape

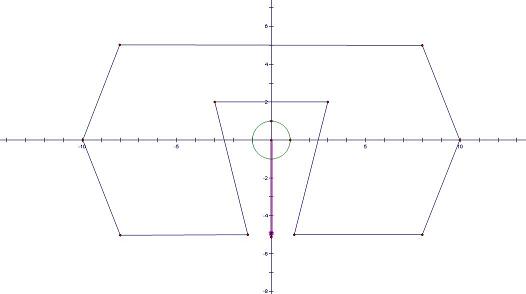
題意：
二維場景內
給定一個 半徑 = R，位置 = (0,0) 的圓
及 N 個多邊形障礙物
問，是否在存一個移動方向，使得當圓形以直線前進時
不會觸碰這些障礙物

分析：
算法大約都是枚舉（離散的）移動方向/角度 - angle[M]
然後逐一判斷是否可行

有關「觸碰」的限制
雖然可以 ± Epsilon 處理
但這會令代碼變得噁心

為此，Those 提出了一個相當漂亮的做法：
1) 對角度排序 - angle[M]
2) 使用前進方向： (angle[i] + angle[i+1]) * 0.5

算法－枚舉移動方向 (angle[M])：
對每頂點，作點到圓切線（共兩條）
這些切線方向就是要枚舉的移動方向

算法－判斷：
給定移動方向 - Y
不能逃逸 ⇒ 圓形軌跡觸碰其中一個多邊形 ⇒ 圓形軌跡觸碰其中一段邊

所以先是想到了線段/多邊形相交之類的方法

但想多一會，其實可以利用圓形為凸的性質：

Y := 前進方向 (單位向量)
X := 與 Y 垂直的單位向量
對每項線段：P → Q
1) 若 P → Q 不在 圓形前方
Continue
2) 投影 P → Q 至 X，得到閉區間 [A, B]
若 [A, B] ∩ [-R, R] ≠ ∅
Return 逃逸失敗
Return 逃逸成功

1) 計算內積 P · Y 及 Q · Y
2) 計算內積 P · X 及 Q · X

怨言：
這題提交了數次... 重覆地 WA
當我 code 了第二種相當不同的算法
經調試後提交，還是返回 WA 時
我才想起，Those 最後的一個 bug，是忘了處理 N = 0 的情況... ... ... ...！
（前天我在聽到後還在笑...）

第二段 Code 改了... 提交... ... TLE
第一段 Submitted Code 改了... 提交... AC
（現在我完全明白他的無奈了）