PKU 2416 Return of the Jedi

題意：

在平面上，給定 N (≤ 10) 個圓（任何兩圓不相交／觸碰）
及 A、B 兩點

求最短 A 到 B 路徑（不得進入任何圓形內，但可以觸碰）的長度

---

應用知識：

此題基本上是一道 2D Geometry Exercise
只是在 公式推導 及 處理 Boundary Cases 時要比較小心...

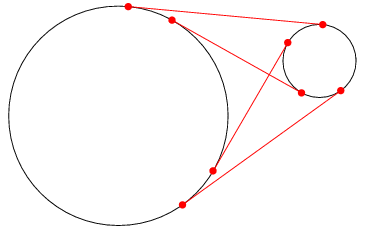
1. 圓到圓切線（全４種）
2. 點到圓切線
   
3. 判斷 線段／圓 交點
   
4. 最短路算法

2. 的計算可透過 1. 完成
── 把 點 看為 半徑 = 0 的圓

---

算法：

最短路必定由以下部份組成：

• 圓到圓切線
• 點（A 或 B）到圓切線
• 線段 AB
• 圓上的弧（其端點必定為上述三項的端點）

註：上列首三項
有與任何一圓正規相交（Properly interesect）者
排除在建圖考慮之外

故可構作圖 G := {V, E}
V := {A, B, 切線端點}
E := 切線／線段／弧長度

答案 := A 到 B 最短路

一種實現的方法：

1. O(N²) 枚舉所有 Tangent - P_startP_end
2. For 每一條 Tangent，用 O(N) 時間檢查有沒有與其它圓正規相交
   若果沒有，給 P_start 及 P_end 一個 int 值作為 node ID（可考慮使用 STL 的 map），連一條 tangent 長度的 edge
   
3. For 每一個圓形，找出所有在其圓周上的 Tangent 端點，每一 pair 連一條 Arc 長度的 edge

時間複雜度 O(N³)