[2D Geometry] 內/外 兩圓公切線 的對應

2010-08-23 2am 更新：

1. 兩種 圓/圓公切線 (Common Tangent)，正名為
   a) 「外公切線」(Common External Tangent)， 及
   b) 「內公切線」(Common Internal Tangent)
   下面討論一律略去「公」 ("Common") 一字
   ....嗯... 外公切線... 以下簡稱為「外切線」及「內切線」
2. 兩圓切線共有 5種情況 ...
   我正在驗證本 Entry 所提供的 Implementation 能否覆蓋全部情況
   ──別被嚇到... 本人直觀地認為本 Entry 所討論的 Implementation
   已能覆蓋所有情況，只是仍有待證實

---

昨晚隨便在 Ural Timus OJ 上選了一道幾何 ── Ural 1340 Cucaracha
想出了某 case 的算法後
發現自己不懂怎樣計算某一角度
只懂得 BSearch... 然後又發現 BSearch 不行...

再細心一想
才發現這個問題其實可以 reduce 至「點到圓切線」...

---

那我就想起... 原來我還沒有一份「點到圓切線」的 Code Template...

在這次之前不知道推導過這公式多少次...
雖然每次都能推出，但推導過程會花費相當長的時間
所以實在太有必要寫一份武器（要不，就把公式推導到爐火純青的熟練程度）

上回在 這篇Entry 談過
「點到圓切線」是「圓到圓切線」的特例 ── 其中一圓半徑=0

而「圓到圓切線」在一般情況下共有 4條

 

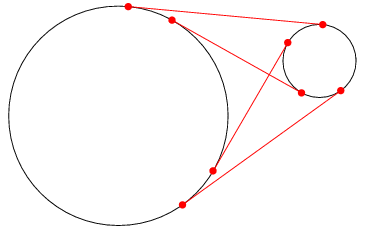
分 「外切線」(External Tangent) 及 「內切線」(Internal Tangent) 兩種

──註：上行此兩項述語這是本文的定義，自行定義的原因一是為方便以下的說明
二是因為在 Google 暫時搜不出相關的述語...

而每種切線各有 2條

那 code template... 就是寫！

寫呀寫的...
突然有一個驚喜的新發現（潮左勿 WoW）：

「內切線」原來是「外切線」的特例！

Codeforces #26 (Codeforces format)

2010-08-16 Mon
HKG Time - 2300 to 2500

• 題目在這
• Standings（大scoreboard）
• Room 10 Scoreboard（My room） 

---

Codeforces format：

留意標題後的括號 - Codeforces format

比賽模式跟 SRM 很相似：

• 難道不同的題目分數不同：
  (A,B,C,D,E) = (500, 1000, 1500, 2000, 2500)
• Submit 時間愈早分數愈高
• 比賽完結時才進行 System Test

不過亦有不同的地方：

SRM 479

同房又見 rng_58 ...

---

250 是一道 模擬+貪心
實踐算法花了相當長的時間（主要是卡在 index）
（眾參賽者的 submission 亦相當慢）

500 的數據範圍很大，就我而言是毫無頭緒
到中後期... 見這麼多人 (約 150 ／ 600) submit 500
看來這次要下跌了...

1000 就更不用說了... 懶得開
（最後沒有人解掉此題）

---

Challenge Phase 期間
發現一個複雜度 O(44777777 × 50 × 2) 的 solution
猶疑了一兩分鐘，把 code 關掉再開...
始終自己分數太低... 還是 不敢 Cha

後來這段 code 被Cha 至 TLE 了...

2010-08-10 Team Training - NWERC 2002

2010-08-10 Tue
HKG Time - 1900 to 2400

• 題目在這
• On Site Scoreboard
• Official Solution

---

這次的題目不算太難（8年前的舊題目...）
在訓練前預先知道這份題目當中有一道難題（題E）
略過此題，其它的幾乎全部做了出來

今天我們 team （= Joe + Kn + Bill） solve 了 6 題
另一 team （= Chin + Danny + Hao + Jian）也不錯，同樣 solve 了 6 題
而超超到後期不肯做題... - -

飲恨是 Joe 的 題G... 我沒能幫甚麼... 他只差一點點

---

Problem A: ICPC 2670 Euro Efficiency

解(Joe)：簡單 DP

令 DP[X] := 完成 $X 的交易，所需最少的硬幣個數（包括「給」和「找」）
注意：需要計算 DP[1..N]，其中 N > 100

沒有仔細想 N 最 tight 的上界... 當時隨便選了 40000 便算了

---

Problem B: ICPC 2671 Markov Trains

解(Kn)：超暴力 DFS!!

DFS 窮舉所有 strategy（即規劃路線）
分別計算各種情況（窮舉班次 miss / arrive 的可能性）下
最後以 map<string,int> 記錄 probability
── 每次 DFS至目的地時，遞加：map[s] += prob;

想過 DP，但題目對 strategy 的定義...
例如 路線容許 重覆經過同一個 city、班次開出與否有 uncertainty

似乎不太可能發現 strategy 的無後效性

當時 Chin 的 team 把這題 AC 了...
然後還一度以題數超越了我們
所以我們也一定把此題做出來

正當我在擔心這算法能否在時限內水過之際...
居然 0.016 sec 極速 WA（然後也極速 AC） 了...

---

Problem C: ICPC 2672 Hansel and Grethel

解(Kn)：簡單 2D 幾何

SRM 478

不錯!! 雖然 ratiing 只是微昇
但, 終於到達 90 percentile 了!!
(rating 亦創下新高)

只是... 過程有點悲劇...

---

250

看到 problem statement 的第一個字 ── Rabbit
出題者是誰... 心裏大概有個譜... 知道要小心應對...
讀完整題以後... 果然沒有平日SRM般... 算法即時浮現的感覺...

由那兩條詭異的算式...
只能估計是數學題...

在沒有 idea 的情況下
挑了 init = 1 的情況
暴力 simulate 頭幾個 step 的所有 configuration...
發現... e?!
這, 花了 5 分鐘左右

然後... 考慮 init 不等於 1 時讓怎麼處理...
這, 花了 5 分鐘左右

然後... 在算法基本上成形的狀況下...
寫 code... run...
然而... 運行 sample 2 和 3
跟 correct output 比較... 死活相差 1...

2010-08-03 Team Training - SWERC 2005

(整理中)

• 題目在這
  
• On Site Scoreboard
• Test Data + Reference
• 官網在這

這次的 SWERC 的題目
比起上兩次的 CEPC 輕鬆多了

今天我們 team （= Joe + Kn + Bill） solve 了 6 題
（Gagguy 獨力 solve 了 7 題!!）

飲恨是 Joe 的 題G... 只差一點點
題F 沒有想出算法... 這個有點過不去
題I 剛剛 AC了... 原來 problem statement 想暗示 test data 很弱
題J 也 AC 了... 算法不太難想，理論上應該也可以 AC 的...但前提是前幾題要做得足夠快

---

Problem A: ICPC 3502 The mysterious X network (Bill)

解：水題 ── BFS

---

Problem B: ICPC 3503 Bin Packing (Bill)

解：水題 ── 貪心

---

Problem C: ICPC 3504 On Storing Clothes (Kn)

解：簡單模擬


要小心的 Case 包括 一次過掛 N-1 件衣服 

Voronoi diagram, Delaunay triangulation and 3D Convex Hull

(Still refinining... this blog entry. More images will be added to aid understanding... hopefully)

Introduction:

In the following discussion, Voronoi diagram and halfplane intersection refer to the 2D case, unless otherwise specified.

I hope I can list some nice properties of as well as some relationships between the following three structures in computational geometry:

• Voronoi diagram
  
  
  
  [You need to understand what is going on on the right image.The left and the middle will be discussed below.]
• Delaunay triangulation
• 3D convex hull