即使一些當中 Take 過 Number Theory 課的
似乎亦未能將知識比較皮毛的部份運用自如...
上星期四 Chin 講一下 Phi Function,Primitive Root 及 Discrete Logarithm 的一些應用及題目
再加上做過幾道題目以後:
貌似終於對這類課題(尤其是 Phi Function)比較有感覺
所以... 在今天的個人Training 特意挑了 (比較多) Number Theory 的題目,大家一起做
不過... 呃... 感覺大家做的時候比較絕望,所以更加要練習!
Problem A: PKU 3766 Hexagon Coin Toss
問:給定一些類似下圖所示,由邊長為 1 的正六邊形組成的 "M x N" 棋盤。現有一單位圓(直徑 < 1)隨機出現,其圓心必定在棋盤內,求該圓覆蓋 1, 2, 3 格的概率
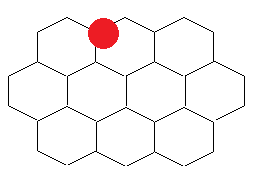
解:畫圖直接分析... 可以參考 Roba 的 blog
Problem B: PKU 1061 青蛙的约会
問:求最小的 x 使得 vx = d (mod n)
解:擴展歐基里德算法(Extended Euclidean Algorithm)
Problem C: PKU 3358 Period of an Infinite Binary Expansion
問:求當 a/b 表示為2進制時,最短循環節的長度,及循環開始的位置
解:Phi Function。推導出來的式子跟 PKU 3696 The Luckiest number 那時幾乎一樣,可以參考 舊文... (有時間再寫一下推導過程...)
按1:所有情況下,即使是 1/8,循環節依然 ≥ 1!
按2:呃... 這道題在 ICPC Live Archive 上面也有,不過數據很水。今次 Training 沒選 PKU 的,然後不少人以 O(答案) 的算法水過,失去了某些意義... ~_~
Problem D: UVa 10692 Huge Mod
問:給個例子說明吧...

在 mod 左邊的數字值 ≤ 10000,最多 10 個
解:呃... 還未做,不過大概是統計形如 {ai mod N} 的循環節長度。(鴿巢原理 ⇒ 循環節長度 ≤ 10000 ⇒ 可枚舉)實現涉及 Recursion,感覺比較噁心...
Problem E: PKU 1997 Word Puzzle
問:題目有點長... 自己看吧
解:以 Trie 記錄 pattern。對表格每個位置,分別朝上下左右 etc八個方位掃描,檢查能否找到 任何 pattern。
Joe 說能用 AC自動機 加快,但本人對這東西不了解
沒有留言:
發佈留言