今天仍然選了比較難的題
6題之中,在4小時內只把3題做出來... 感覺有點差...-_-
Parsing (題A) 及 Greedy (題F) 卡了太久... 沒有時間做剩下的題
還好最後仍然把那道 2D Geometry (PKU 2036!) 做出來...
今次的題目涵蓋了 2D Geometry、Parsing/String Processing、Simulation、DP、Integration,算是相當全面,而且比較煩。在考驗編程技巧同時,亦要求謹慎小心。值得一提的是,自己在 PKU 2065(題F) 學了一樣很多人早已知道的事實(見下)。
這一 set題目 是比較難+煩... 所以表現不理想大家也不要灰心!
Problem A: PKU 2372 D++ Again
問:(講起我就扯火...)自己看!這題目就是考驗閱題!
(縱使 AC 過後我依然覺得題目寫得不夠清楚...-_-)
注:最後栽在這 Test Case...
"(*(**)" - YES
2010年6月30日星期三
2010年6月28日星期一
PKU 2416 Return of the Jedi
題意:
在平面上,給定 N (≤ 10) 個圓(任何兩圓不相交/觸碰)
及 A、B 兩點
求最短 A 到 B 路徑(不得進入任何圓形內,但可以觸碰)的長度
應用知識:
此題基本上是一道 2D Geometry Exercise
只是在 公式推導 及 處理 Boundary Cases 時要比較小心...
- 圓到圓切線(全4種)
- 點到圓切線
- 判斷 線段/圓 交點
- 最短路算法

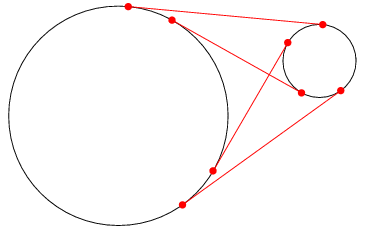
2. 的計算可透過 1. 完成
── 把 點 看為 半徑 = 0 的圓
2010年6月27日星期日
[練習] SRM 473
250
Bounded ⇔ 走四個循環 返回起點500
圓周上平分佈的N點中,任取三點成一直角三角形⇔ 其中兩點連起來是直徑
所以問題轉化為統計直徑數目,M
答案 := M × (N - 2)
直接應用公式 + while-loop mark visited 選點
在最壞情況會很慢 (?)
建議實現一種類似 Linked List 的 Disjoint Set
FOR(i,0,n) parent[i] = i;
FOR(i,0,m) {
LL j = (a*i*i + b*i + c) % n;
j = find(j); // Find parent
vis[j] = 1;
parent[j] = find((j+1)%n);
}
Topcoder Open 2010 - Round 2
上一次 Round 1 跟 rng_58 同房
今次 Round 2 跟 ACRush 同房
比較慢地把 250 做出來
而那 500 的算法... Ad-hoc 到不得了
在完結前 2 min 才通過樣例並提交
結果被 cha
瓜了...
諷刺的是 rating 微升...
是因為本來的 rating 就很低的關係吧...
判定 Connecteness
Connected ⇒ Graph 是 Euler Cycle ⇒ 邊權值總和
(這裏我對於 Odd/Even degree 想了一陣子...)
Disconnected ⇒ Return -1
有好幾種算法... bsearch, monotonicity, by case 處理...
說一下 bsearch 的...
Generate 所有 由單數 digit 組成的數字 - A[N] (N = O(58))
對於 i := 0 to N-1
(二分)查找最少的 A[j]
使得 A[i] + A[j] >= X
記錄最小的 A[i] + A[j]
⇒ O(N lg N)
──自己居然連如此標準 + 簡單的算法都想不出...
實在要好好反省一下... ... ... ...
今次 Round 2 跟 ACRush 同房
比較慢地把 250 做出來
而那 500 的算法... Ad-hoc 到不得了
在完結前 2 min 才通過樣例並提交
結果被 cha
瓜了...
諷刺的是 rating 微升...
是因為本來的 rating 就很低的關係吧...
250
判定 Connecteness
Connected ⇒ Graph 是 Euler Cycle ⇒ 邊權值總和
(這裏我對於 Odd/Even degree 想了一陣子...)
Disconnected ⇒ Return -1
500
有好幾種算法... bsearch, monotonicity, by case 處理...
說一下 bsearch 的...
Generate 所有 由單數 digit 組成的數字 - A[N] (N = O(58))
對於 i := 0 to N-1
(二分)查找最少的 A[j]
使得 A[i] + A[j] >= X
記錄最小的 A[i] + A[j]
⇒ O(N lg N)
──自己居然連如此標準 + 簡單的算法都想不出...
實在要好好反省一下... ... ... ...
2010年6月25日星期五
PKU 3679 The Delivery of Control
題意:
給定 H x W 帶號整數二維陣列 (H, W ≤ 20)
現在要在其中走一個圈,周界 ≤ K (≤ 20)
(路線是 grid 的 edge,每走一條周界 += 1)
圈不可以 self-touch
計算被包圍的元素值的總和
求最大總和
不合法 shape 的樣例:
- 需要連接
- ◎ ◎
- 不可以角碰角
- ◎◎
◎ ◎
◎◎◎ - 剛剛才想到:角碰角 ⇒ 有洞
所以不需要另寫程序作處理 - 不可以有洞 1 (周界 = 16)
- ◎◎◎
◎ ◎
◎◎◎ - 不可以有洞 2 (周界 = 20)
- ◎◎◎
◎ ◎
◎ ◎
◎◎◎
昨晚(強迫)Leo 及 Chin 跟我討論這條比較少人AC 的題目
然後今天下午... 和 Joe 分別起手 code...
慶幸是挑戰成功了(雖然非常懷疑自己是水過)
嗯... 看見 range 及 10秒 時限 便想到 Searching 吧...
不過起初我還妄想能否用狀態 DP 解決
然後被一大堆不知怎麼處理的狀況解決了... orz
(當然,我不排除 DP 的可行性...)
所以只好 code 搜索
2010年6月23日星期三
2010-06-22 Individual Training
上星期二發現大家的 Number Theory 比較弱...
即使一些當中 Take 過 Number Theory 課的
似乎亦未能將知識比較皮毛的部份運用自如...
上星期四 Chin 講一下 Phi Function,Primitive Root 及 Discrete Logarithm 的一些應用及題目
再加上做過幾道題目以後:
貌似終於對這類課題(尤其是 Phi Function)比較有感覺
所以... 在今天的個人Training 特意挑了 (比較多) Number Theory 的題目,大家一起做
不過... 呃... 感覺大家做的時候比較絕望,所以更加要練習!
Problem A: PKU 3766 Hexagon Coin Toss
問:給定一些類似下圖所示,由邊長為 1 的正六邊形組成的 "M x N" 棋盤。現有一單位圓(直徑 < 1)隨機出現,其圓心必定在棋盤內,求該圓覆蓋 1, 2, 3 格的概率
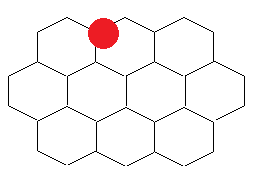
解:畫圖直接分析... 可以參考 Roba 的 blog
Problem B: PKU 1061 青蛙的约会
問:求最小的 x 使得 vx = d (mod n)
解:擴展歐基里德算法(Extended Euclidean Algorithm)
Problem C: PKU 3358 Period of an Infinite Binary Expansion
問:求當 a/b 表示為2進制時,最短循環節的長度,及循環開始的位置
解:Phi Function。推導出來的式子跟 PKU 3696 The Luckiest number 那時幾乎一樣,可以參考 舊文... (有時間再寫一下推導過程...)
按1:所有情況下,即使是 1/8,循環節依然 ≥ 1!
按2:呃... 這道題在 ICPC Live Archive 上面也有,不過數據很水。今次 Training 沒選 PKU 的,然後不少人以 O(答案) 的算法水過,失去了某些意義... ~_~
Problem D: UVa 10692 Huge Mod
問:給個例子說明吧...

在 mod 左邊的數字值 ≤ 10000,最多 10 個
解:呃... 還未做,不過大概是統計形如 {ai mod N} 的循環節長度。(鴿巢原理 ⇒ 循環節長度 ≤ 10000 ⇒ 可枚舉)實現涉及 Recursion,感覺比較噁心...
Problem E: PKU 1997 Word Puzzle
問:題目有點長... 自己看吧
解:以 Trie 記錄 pattern。對表格每個位置,分別朝上下左右 etc八個方位掃描,檢查能否找到 任何 pattern。
Joe 說能用 AC自動機 加快,但本人對這東西不了解
即使一些當中 Take 過 Number Theory 課的
似乎亦未能將知識比較皮毛的部份運用自如...
上星期四 Chin 講一下 Phi Function,Primitive Root 及 Discrete Logarithm 的一些應用及題目
再加上做過幾道題目以後:
貌似終於對這類課題(尤其是 Phi Function)比較有感覺
所以... 在今天的個人Training 特意挑了 (比較多) Number Theory 的題目,大家一起做
不過... 呃... 感覺大家做的時候比較絕望,所以更加要練習!
Problem A: PKU 3766 Hexagon Coin Toss
問:給定一些類似下圖所示,由邊長為 1 的正六邊形組成的 "M x N" 棋盤。現有一單位圓(直徑 < 1)隨機出現,其圓心必定在棋盤內,求該圓覆蓋 1, 2, 3 格的概率

解:畫圖直接分析... 可以參考 Roba 的 blog
Problem B: PKU 1061 青蛙的约会
問:求最小的 x 使得 vx = d (mod n)
解:擴展歐基里德算法(Extended Euclidean Algorithm)
Problem C: PKU 3358 Period of an Infinite Binary Expansion
問:求當 a/b 表示為2進制時,最短循環節的長度,及循環開始的位置
解:Phi Function。推導出來的式子跟 PKU 3696 The Luckiest number 那時幾乎一樣,可以參考 舊文... (有時間再寫一下推導過程...)
按1:所有情況下,即使是 1/8,循環節依然 ≥ 1!
按2:呃... 這道題在 ICPC Live Archive 上面也有,不過數據很水。今次 Training 沒選 PKU 的,然後不少人以 O(答案) 的算法水過,失去了某些意義... ~_~
Problem D: UVa 10692 Huge Mod
問:給個例子說明吧...

在 mod 左邊的數字值 ≤ 10000,最多 10 個
解:呃... 還未做,不過大概是統計形如 {ai mod N} 的循環節長度。(鴿巢原理 ⇒ 循環節長度 ≤ 10000 ⇒ 可枚舉)實現涉及 Recursion,感覺比較噁心...
Problem E: PKU 1997 Word Puzzle
問:題目有點長... 自己看吧
解:以 Trie 記錄 pattern。對表格每個位置,分別朝上下左右 etc八個方位掃描,檢查能否找到 任何 pattern。
Joe 說能用 AC自動機 加快,但本人對這東西不了解
2010年6月19日星期六
PKU 1952 BUY LOW, BUY LOWER
Problem Statement:
給定陣列 A[N], 其中 1 ≤ A[i] ≤ 215-1
求最長嚴格下降序列 (Strictly Longest Decreasing Subsequence) 的長度及方法數
當序列元素完全相同,則兩個方法視為一樣(見樣例)
Sample Input:
Sample Output:
題目最難之處就是要避免重計
其中一個有效方法就是以元素的值作為狀態
為此,自己的第一個 AC Submission 就加入了三項預處理...
寫的很累贅...
後來 Google 了一下
發現自己沒有用到一項已經發現的 Observation:
給定陣列 A[N], 其中 1 ≤ A[i] ≤ 215-1
求最長嚴格下降序列 (Strictly Longest Decreasing Subsequence) 的長度及方法數
當序列元素完全相同,則兩個方法視為一樣(見樣例)
Sample Input:
12
68 69 54 64 68 64 70 67 78 62 98 87
1 1 2 2 2 3 1 3 1 4 1 2 // Explaination
69 68 64 62
69 68 67 62
Sample Output:
4 2
題目最難之處就是要避免重計
其中一個有效方法就是以元素的值作為狀態
為此,自己的第一個 AC Submission 就加入了三項預處理...
寫的很累贅...
後來 Google 了一下
發現自己沒有用到一項已經發現的 Observation:
2010年6月16日星期三
[進階DP] 基於連通性狀態壓縮的動態規劃問題
看完 男人八題 的 題C:Tony's Tour 以後
[I like the title: "做男人不容易系列:是男人就过8题--LouTiancheng题"]
即時想起:
ICPC World Fianls 2010 - Problem I : Robots on Ice

連結:
1) 《基于连通性状态压缩的动态规划问题》 By Cdq(陈丹琦)
2) 【动态规划】Ural1519 Formula 1 - By ccy1991911
這是Google 返回的 Blog 文...
感覺寫的挺用心(未詳閱)
3) 【专辑】插头DP
NotOnlySuccess 寫的
插個花:
雖然自己都幾鐘意之前呢個黑底白字既 theme
而且感覺亦幾 Professional =v=
不過望落去時對眼真係有啲辛苦... 所以都係轉番白底黑字好啲
呀... 另外一個原因係 LaTeX 冇黑底白字(好似係)
呃... 暫時黎講個 blog 都仲係寫得冇乜系統
究竟寫 Technical Term 用中定英好呢?
白話文定書面語好呢?
[I like the title: "做男人不容易系列:是男人就过8题--LouTiancheng题"]
即時想起:
ICPC World Fianls 2010 - Problem I : Robots on Ice

連結:
1) 《基于连通性状态压缩的动态规划问题》 By Cdq(陈丹琦)
- 插頭 DP
- 括號表示法(好似係)
- Hamiltonian Path
2) 【动态规划】Ural1519 Formula 1 - By ccy1991911
這是Google 返回的 Blog 文...
感覺寫的挺用心(未詳閱)
3) 【专辑】插头DP
NotOnlySuccess 寫的
插個花:
雖然自己都幾鐘意之前呢個黑底白字既 theme
而且感覺亦幾 Professional =v=
不過望落去時對眼真係有啲辛苦... 所以都係轉番白底黑字好啲
呀... 另外一個原因係 LaTeX 冇黑底白字(好似係)
呃... 暫時黎講個 blog 都仲係寫得冇乜系統
究竟寫 Technical Term 用中定英好呢?
白話文定書面語好呢?
PKU 3696 The Luckiest Number
題意:
給定 L
求 集合 { 8, 88, 888, ... ,888888, ... } 當中 能整除 L 的最小的一個數字
列印該數的長度
算法 ── 思路:
設該數為 88....8,則有方程:
8 × 11....1 ≡ 0 (mod L) -----------(1)
設 g := (8, L),得:
8/g × 11....1 ≡ 0 (mod L/g) -----------(2)
Case 0: L/g = 1
...
Case 1: L/g 整除 2 或/和 整除 5
11....1 顯然不能整除 2 或/和 整除 5 ⇒ 無解
Case 2: 其他情況
由於 (8/g, L/g) = 1,(2) 可以化簡為:
11....1 ≡ 0 (mod L/g) -----------(3)
以下為最關鍵的一步!
給定 L
求 集合 { 8, 88, 888, ... ,888888, ... } 當中 能整除 L 的最小的一個數字
列印該數的長度
算法 ── 思路:
設該數為 88....8,則有方程:
8 × 11....1 ≡ 0 (mod L) -----------(1)
設 g := (8, L),得:
8/g × 11....1 ≡ 0 (mod L/g) -----------(2)
Case 0: L/g = 1
...
Case 1: L/g 整除 2 或/和 整除 5
11....1 顯然不能整除 2 或/和 整除 5 ⇒ 無解
Case 2: 其他情況
由於 (8/g, L/g) = 1,(2) 可以化簡為:
11....1 ≡ 0 (mod L/g) -----------(3)
以下為最關鍵的一步!
2010年6月9日星期三
South America 2009
Solved 10 out of 11
Penalty 輸俾 on site champion 幾十
今日表現唔錯!
題目較淺
80分鐘 KO 7題
Nope... 喺 UVa 見到啲 Statistic
人地單挑出嚟既成績都接近我地一team人做出黎既成績...
飲恨係kick喺條 F - Suffix Array...
感覺明明algo冇錯
double check 過... 武器冇打錯...
又整唔出test case戳得死佢
Penalty 輸俾 on site champion 幾十
題目較淺
80分鐘 KO 7題
Nope... 喺 UVa 見到啲 Statistic
人地單挑出嚟既成績都接近我地一team人做出黎既成績...
| # | Solved | Score | A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hussar | 10 | 1055 | 1/48 | 1/56 | -/- | 2/37 | 1/69 | 3/224 | 2/202 | 3/159 | 2/27 | 1/13 | 1/80 |
| GAGGUY+AC | 10 | 1354 | 1/33 | 1/43 | -/- | 4/296 | 3/37 | 1/244 | 1/165 | 1/203 | 1/62 | 1/54 | 1/117 |
| Prof. QQ | 8 | 1361 | 2/117 | 2/73 | -/- | 1/67 | 3/150 | -/- | -/- | 5/303 | 6/152 | 1/7 | 3/192 |
| BDJ | 8 | 1367 | 1/206 | 1/117 | -/- | 2/130 | 3/72 | -/- | 1/- | 3/282 | 4/144 | 1/16 | 3/200 |
飲恨係kick喺條 F - Suffix Array...
感覺明明algo冇錯
double check 過... 武器冇打錯...
又整唔出test case戳得死佢
2010年6月8日星期二
幾道水題
Ural 1280 Topological Sort
對拓撲順序的理解
Ural 1282 Game Tree
不錯的 Mini-Max 入門題目
(自己是第一次做這種題目)
Ural 1296 Hyperjump
基本DP
PKU 3316 Snakes on a Plane
模擬;個人認為挺多陰險的 Case
PKU 2418 Hardwood Species
字典樹
注:數據不符合描術,字符不限於字母及空格!
測試證實字符的ASCII code 小於 128
對拓撲順序的理解
Ural 1282 Game Tree
不錯的 Mini-Max 入門題目
(自己是第一次做這種題目)
Ural 1296 Hyperjump
基本DP
PKU 3316 Snakes on a Plane
模擬;個人認為挺多陰險的 Case
PKU 2418 Hardwood Species
字典樹
注:數據不符合描術,字符不限於字母及空格!
測試證實字符的ASCII code 小於 128
2010年6月7日星期一
IPSC 2010 (Live)
| 60. | Hussar | 21 | 2465 | A1 A2* B1 B2 C1* C2 D1**** F1* F2* I1***** I2 J1** J2 K1 L1 |
Hussar 在完全不知道比賽規則
及遲了 30+ 分鐘開始的情況
得到第60名... 算是不錯吧
值得一提的是,在最後2分鐘找到 Bug:
我把一句的 feq (floating point ==) 打錯為 flt (floating point <) 改正後用了1分鐘提交 I1
然後用了1分鐘下載 I2 的 input
最後在完結前18秒 提交 I2
通過!!
這個 bug 足足花了接近一小時去發現...
有時間再打一下我懂的題目...
訂閱:
留言 (Atom)